优化算法(一)： SCA算法
发布时间：2024-04-29 03:59:46 浏览次数：
萌新，本科生（双非），在实验室混了一年，学了几个优化算法在此写一下总结，分析一下心得，也期望着有大佬可以来一起交流。
- 基本思想
SCA算法是一种新颖的全优化算法，是由澳大利亚学者Mirjalil为优化飞机机翼设计问题而提出的，它基于数学中正弦/余弦函数图像的概念，使最佳解可以向内或向外扩展，而且算法本身拥有勘探和开发两个阶段，可以对最佳位置进行深度挖掘，最终达到全局最优的目的。 - 算法步骤
Step 1.
输入总体大小和最大迭代次数
，初始化所有参数，包括
算法中的需区域位置(或移动方向);
运动应朝着目的地或向目的地向外移动的距离;
随机权重值;
表示正弦和余弦均等概率；初始化种群数量
，并提供初始化解空间。
Step 2.
根据参数使用下列公式更新
使用时使用更大的解空间；
时使用较小的解空间。在原文中
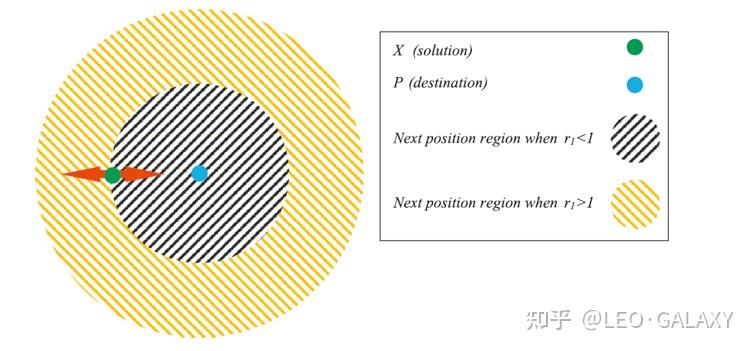
当 时，所谓更大的解空间为算法的探索阶段，当
时，所谓较小解空间为算法开发阶段，无限逼近或者找到最优解。
Step 3.
对于SCA算法而言，算法的开发和探索阶段用到的公式是相同的，但是在开发阶段中，随机解会逐渐变化且随机变化远小于探索阶段的变化。其公式如下：
其中， 是
之间的随机数，使用正弦公式求解和使用余弦公式求解的概率是相同的，向量表示每一维度的目标点。
Step 4.
经过多次迭代，到达规定的条件后停止迭代，返回最佳位置X_D,输出最优值，算法结束。
原算法的基本步骤就这些，SCA算法算是近些年提出的结构比较简单的元启发式优化算法了，下面在说一下SCA算法存在的缺点
3. 算法存在问题
（1） 参数设置的太过简单，可以说
参数具有很大的改进空间，笔者亲自用MATLAB画过
参数的图像，仅为一条节距为2的直线，这种线性直线不能很好的对优化算法的探索和开发起到过渡作用。
（2）算法收敛性不好，过早陷入，这应该是元启发式算法的通病，可以通过引入混沌映射、高斯突变、莱维飞行进行解决，以达到跳出局部最优的作用。
4. 解决工程问题
笔者使用SCA算法进行了两次算法改进，第一次用在了WSN（无线传感网）节点覆盖，另一次用在了WSN簇头数据错误分类（异常检测）。在这里就展开讲了，有兴趣的朋友可以私信讨论。
