MindSpore高阶优化器（2）_首页-摩臣-官方注册指定站

MindSpore高阶优化器（2）

发布时间：2024-03-12 11:58:43 浏览次数：

上篇文章对深度学习训练中的优化器做了背景介绍，链接戳这里。

这篇跟大家分享MindSpore自研优化器THOR(Trace-based Hardware-driven layer-ORiented Natural Gradient Descent Computation)，该优化器在ImageNet上训练ResNet50，使用MindSpore+8 Ascend 910 仅需66.7分钟，当使用256节点时仅需2.7分钟！该优化器已完成论文投稿，被AAAI2020接受，后续会把论文贴出来（补充论文链接https://www.aaai.org/AAAI21Papers/AAAI-6611.ChenM.pdf）。

上一篇中我们已经介绍过一二阶优化器，其中二阶优化器与一阶优化器相比收敛速度更快，但缺点是二阶信息矩阵求逆复杂度高，为 $\\mathrm O(n^3)$ , 其中 n 为二阶信息矩阵维度，当模型参数量为 $n_\ heta$ 时，对应的二阶信息矩阵的大小为 $n_\ heta \ imes n_\ heta$ 。在深度学习模型中， $n_\ heta$ 常常在数百万的量级，此时二阶信息矩阵的逆无法计算。因此如何降低二阶信息矩阵求逆的计算复杂度成为关键问题。

MindSpore针对该问题，提出了自研算法THOR，该算法是基于自然梯度法，对Fisher矩阵做了近似，自然梯度法中的 $\\mathrm Fisher$ 矩阵可以表示为： $F=\\mathrm{E}[\\frac{\\partial \\mathrm{log}p(y|x,\ heta)}{\\partial \ heta}{\\frac{\\partial \\mathrm{log}p(y|x,\ heta)}{\\partial \ heta}}^T]\\\\$

其中 $P(y|x,\ heta)$ 是网络模型的预测分布， $p(y|x,\ heta)$ 是其概率密度， $\ heta$ 是需要网络模型的参数。

那THOR主要做了哪些改进呢，我们一起来看一下：

1. 降低二阶信息矩阵更新频率

通过实验观察 $\\mathrm Fisher$ 矩阵的F范数（Frobenius norm）在前期变化剧烈，后期逐渐变稳定，从而假设 ${\\left\\{ F^k \\right\\}}^{n}_{k=1}$ 是一个马尔可夫过程，可以收敛到一个稳态分布π，其中 $F^k$ 代表第k个迭代时的 $\\mathrm Fisher$ 矩阵。因此，在训练过程中逐步增大 $\\mathrm Fisher$ 矩阵的更新间隔，可以在不影响收敛速度的情况下，减少训练时间。例如在ResNet50中，更新间隔步数随着训练的进行越来越大，到后期每个epoch只需更新一次二阶信息矩阵，如下图所示。

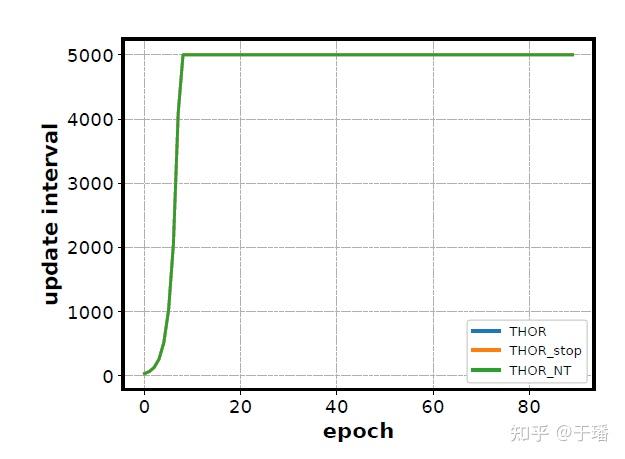
THOR受KFAC启发，将 $\\mathrm Fisher$ 矩阵按层解耦来降低矩阵复杂度，分别针对每一层的 $\\mathrm Fisher$ 矩阵做实验，发现有些层的 $\\mathrm Fisher$ 矩阵趋于稳态的速度更快，因此在统一的更新间隔上，更加细粒度的去调整每一层的更新频率。THOR使用矩阵的迹作为判断条件，当迹的变化情况大于某一阈值时更新该层的二阶信息矩阵，否则沿用上一个迭代的二阶信息矩阵，并且引入了停止更新机制，当迹的变化量小于某个阈值时停止更新该层二姐信息矩阵，且，具体更新公式如下：

$\\Delta^k=\\frac{||tr(F^k_i+\\lambda I)|-|tr(F^{k-1}_i+\\lambda I)||}{|tr(F^{k-1}_i+\\lambda I)|}\\\\$

$\\begin{cases}更新F_i^k ，当?^k∈(w_1,+∞)\\\\ 不更新F_i^k，沿用上一个迭代的F_i^{k-1}，当?^k∈[w_2,w_1]\\\\ 停止更新F_i^k，后期都使用F_i^{k-1}，当?^k∈[0,w_2]\\\\ \\end{cases}\\\\$

2. 硬件感知矩阵切分

THOR在将 $\\mathrm Fisher$ 矩阵按层解耦的基础上，进一步假设每个网络层中的输入和输出块之间也是独立的，例如将每层网络的输入输出切分为n个块，这n个块之间即是独立的，根据该假设对二阶信息矩阵做进一步的切分，从而提高了计算效率。THOR结合矩阵信息损失数据和矩阵性能数据确定了矩阵分块维度，从而大大提升 $\\mathrm Fisher$ 矩阵求逆时间。

那么如何确定矩阵分块维度的呢。具体方法为：

（1）根据 $\\mathrm Fisher$ 矩阵中维度最大的那一层，确定矩阵切分维度，拿ReseNet-50举例，网络层中的最大维度为2048，确定矩阵切分维度为[1,16,32,64,128,256,512,1024,2048]；

（2）根据确定的矩阵维度，根据谱范数计算每个维度下的矩阵损失，具体公式为

$L=1-\\sqrt{\\frac{\\lambda_{max}(\\hat A{\\hat A}^T)}{\\lambda_{max}(A A^T)}}\\\\$

其中 $\\lambda_{max}(X)$ 表示矩阵 X 的最大特征值， A 表示原始未分割矩阵， $\\hat A$ 表示分割后的矩阵。然后统计在该维度下损失小于1%的矩阵数量，最后通过除以总的矩阵数量得到标准化后的矩阵损失信息。

（3）根据确定的矩阵维度，计算每个维度下的矩阵求逆时间，再通过公式 $normalized_n=\\frac{p_1}{p_n}$ 得到每个维度下标准化后性能数据，其中 $p_1$ 表示维度最小的矩阵的性能数据， $p_n$ 表示第n个维度下的性能数据。

（4）根据标注化后的矩阵损失信息和标准化后的性能数据绘图，如以ResNet50为例，可得到下图，图中交叉点为106，与128最接近，最后确定矩阵切分维度为128。

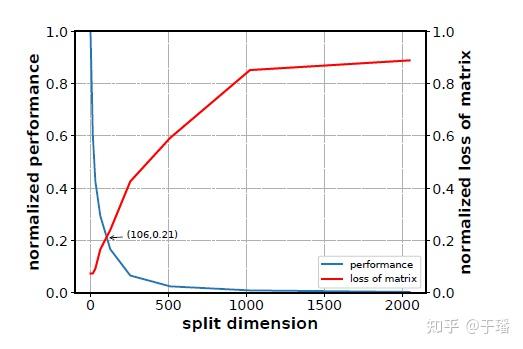
3. 实验结果

下图展示了THOR在ResNet50+ImageNet，batchsize为256时一二阶上的训练曲线图。

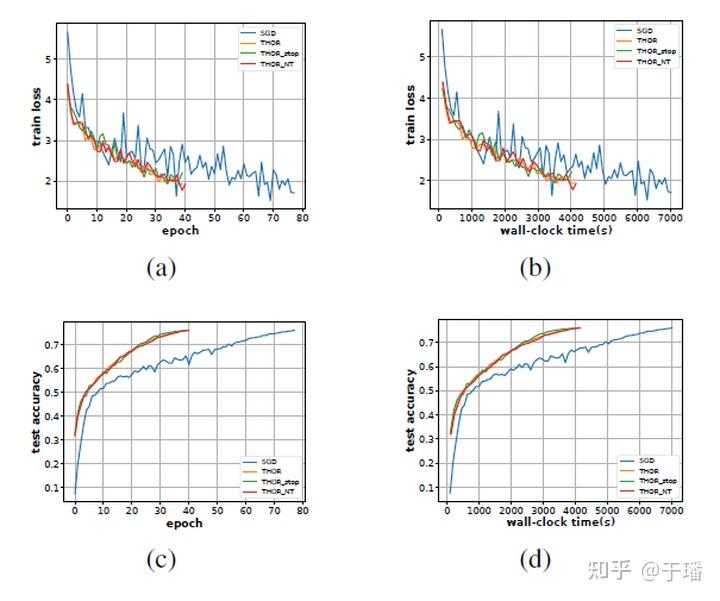
图中的THOR，THOR_stop，THOR_NT分表表示，从图中可以看到THOR收敛所需迭代数大约是一阶的一半，且单step的时间与一阶相差也不大。相比一阶算法需要117min，二阶优化器端到端时间提速约40%。

THOR还测试了在不同batchsize下ResNet50+ImageNet的收敛结果，结果见下表，当batchsize为8192，使用256块Ascend 910时，只需2.7分钟精度即可收敛到75.9%，该结果在业界也是非常有竞争力的。MindSpore团队还会将THOR进一步应用到NLP领域中，如Bert和GPT-3，到时候再跟大家分享THOR在NLP任务上的表现。

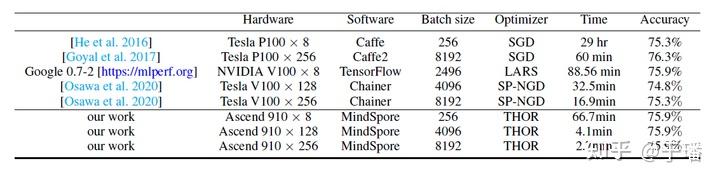
最后做个预告，下一篇跟大家分享下实操经验：如何在MindSpore上使用THOR训练模型？

例行广告时间：）

MindSpore官网：https://www.mindspore.cn/

MindSpore论坛：https://bbs.huaweicloud.com/forum/forum-1076-1.html

代码仓地址：

Gitee-https://gitee.com/mindspore/mindspore

GitHub-https://github.com/mindspore-ai/mindspore

官方QQ群: 871543426

http://weixin.qq.com/r/-0hlfbPEDu5xrfce9x3t (二维码自动识别)

摩臣资讯

MindSpore高阶优化器（2）

发布时间：2024-03-12 11:58:43 浏览次数：