【caffe 深度学习】3.各类优化器介绍
发布时间：2024-03-04 13:00:49 浏览次数：
目录
2.5NAG（Nesterov accelerated gradient）：
tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.ProximalGradientDescentOptimizer
tf.train.ProximalAdagradOptimizer
tf.train.RMSPropOptimizer
?
（1）标准梯度下降法：
标准梯度下降先计算所有样本汇总误差，然后根据总误差来更新权值（可能费时比较严重）
（2）随机梯度下降法：
随机梯度下降法随机抽取一个样本来计算误差，然后更新权值(所以权值更新的方向不保证正确）
批量梯度下降法：
?（3）批量梯度下降法是一个比较折中的方案，从总样本中抽取一定的批次（比如一共有10000个样本，随机抽取100个样本作为一个batch），然后计算这个batch的总误差，根据总误差来更新权值。
?
?
W：要训练的参数
L：代价函数
η：学习率
?
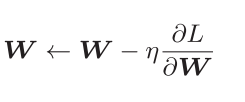
SGD缺点：
1.如果函数的形状非均向，比如呈延伸状，搜索的路径就会非常低效，比如呈“之字形”，它低效的根本原因是梯度的方向没有指向最小值方向。
2.不能逃离鞍点问题、峡谷问题。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
?
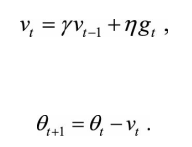gt为当前估计的梯度。这里出现了一个新的变量v,对应于物理上的速度，上面第一个式子表示了物体在梯度上受力，在力的作用下物体速度增加这一物理法则。
当前权值的改变会受到上一次权值改变的影响，类似于小球向下滚动的时候带上了惯性。这样可以加快小球的向下的速度。
优点：
（1）与SGD方法相比，动量方法的收敛速度更快，收敛曲线也更稳定。如图所示：
（2）来到鞍点中心处，在惯性作用下继续前行，从而有机会冲出这片平坦的陷阱。
?
?
前面惯性的获得是基于历史信息的，我们还期待获得对周围环境的感知。
AdaGrad方法对环境的感知是指在参数空间中，根据不同参数的一些经验性判断，自适应地确定参数的学习速率，不同参数的更新幅度是不同的。它的核心思想是对比较常见的数据给予它比较小的学习率去调整参数，对于比较罕见的数据给予它比较大的学习率去调整参数。
实际应用中，我们希望更新频率低的参数可以拥有较大的更新步幅，而更新频率高的参数的步幅可以减小。（比如一个图片数据集，有10000张狗的照片，10000张猫的照片，只有100张大象的照片）。
AdaGrad方法采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性，取值越小表明越稀疏。具体更新公式为：
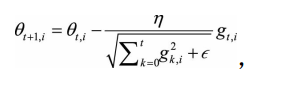
?i：代表第i个分类
?t：代表出现次数
：的作用是避免分母为0，取值一般为1e-8
? η：取值一般为0.01
gk,i表示k时刻的梯度向量gk的第i个维度（方向） 。
分母求和的形式实现了退火的过程，这是很多优化技术常用的策略，意味着随着时间的推移，学习速率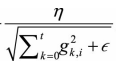
? ? ? ? ? ? ?越来越小，从而保证了算法的最终收敛。
从分母中也可以看出，参数的元素中变动较大的元素学习率将变小（分母变大）。
优点：
（1）Adagrad主要的优势在于不需要人为地调节学习率，它可以自动调节。它的缺点在于，随着迭代次数增多，学习率也会越来越低，最终趋向于0。
（2）可以逃离鞍点问题
Adam方法将惯性保持和环境感知这两个优点集于一身：
（1）Adam记录梯度的一阶矩，即过往梯度与当前梯度的平均，这体现的惯性保持
（2）Adam还记录梯度的二阶矩，即过往梯度平方与当前梯度平方的平均，这体现了环境感知
一阶矩和二阶矩采用类似滑动窗口内求平均的思想进行融合，即当前梯度和近一段时间内梯度的平均值，时间久远的梯度对当前平均值的贡献呈指数衰减。具体来说，一阶矩和二阶矩采用指数衰退平均技术，计算公式为：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
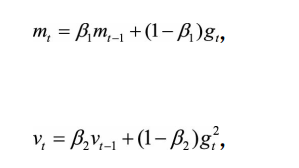
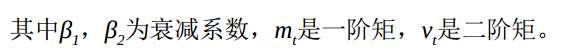
Adam的更新公式为：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
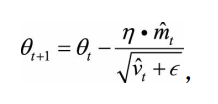
其中：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
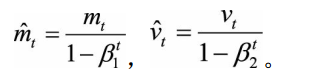
Adam会设置三个超参数，一个是学习率β1、β2标准的设置值分别为：0.9,0.999
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
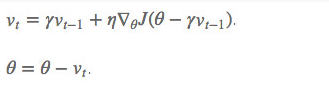
在Momentum中小球会盲目地跟从下坡的梯度，容易发生错误，所以我们需要一个更聪明的小球，这个小球提取知道它要去哪里，它还要知道走到坡底的时候速度慢下来而不是冲上另一个坡。γvt-1会用来修改W的值，计算W-γvt-1可以表示小球下一个位置大概在哪里。?从而我们可以提取计算下一个位置的梯度，然后使用到当前位置。
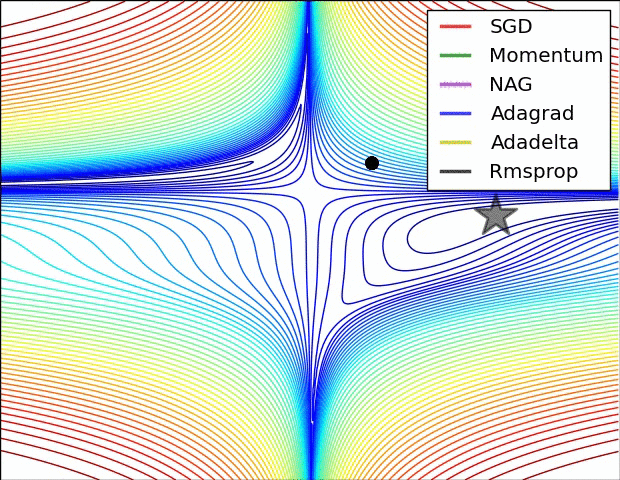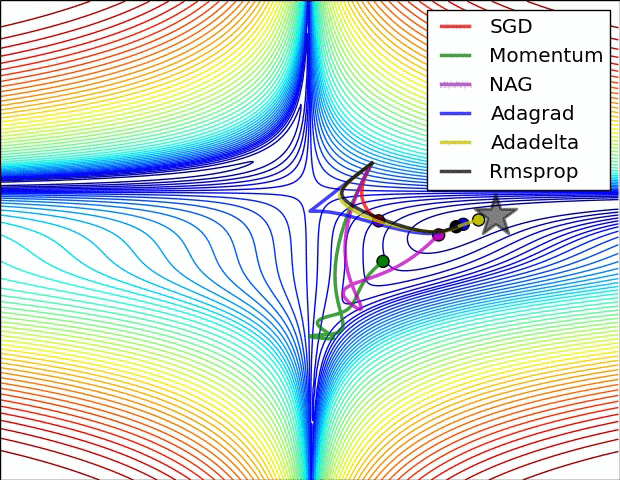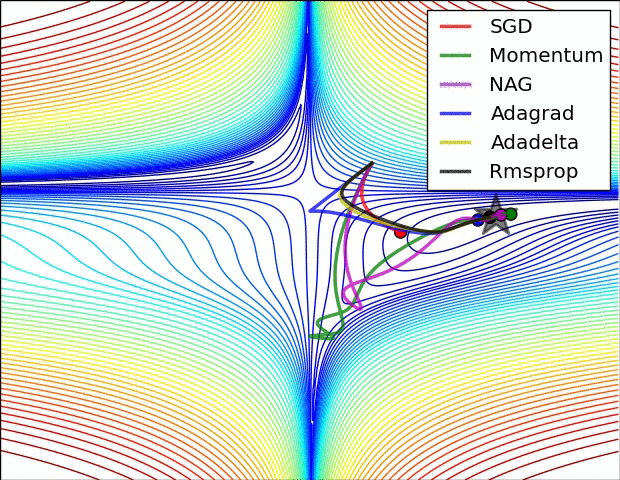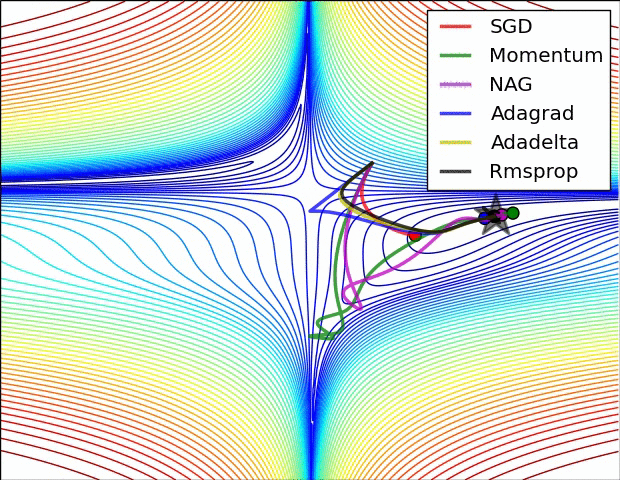
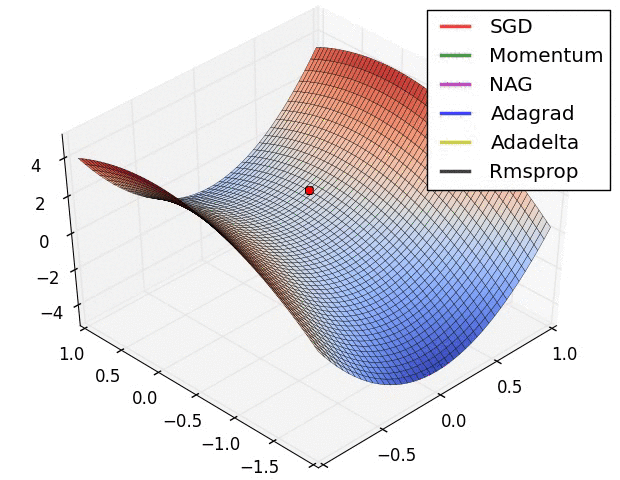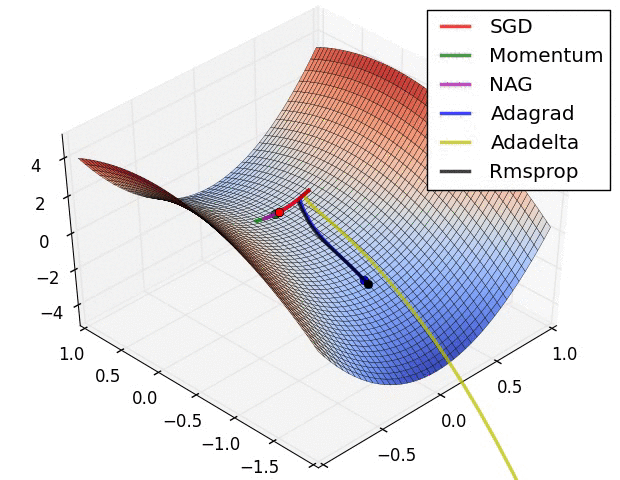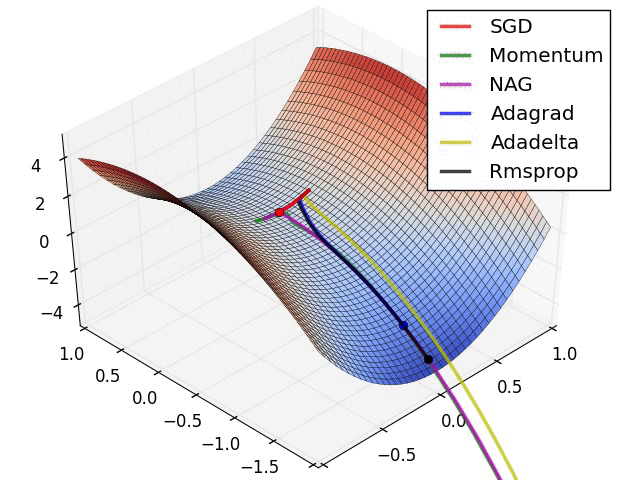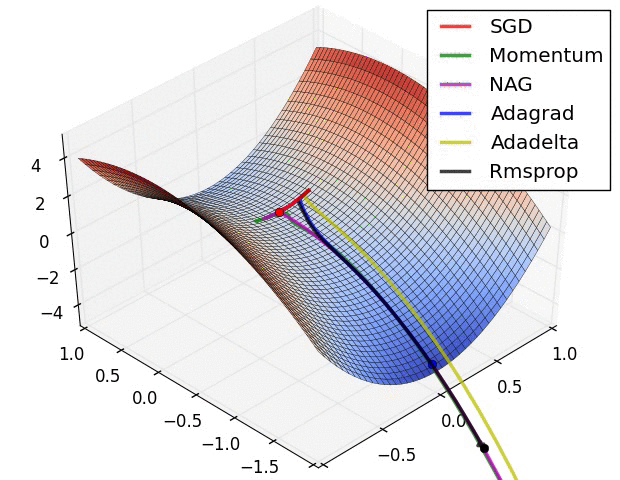
效果对比：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
蓝色是 Momentum 的过程，会先计算当前的梯度，然后在更新后的累积梯度后会有一个大的跳跃。?
而 NAG 会先在前一步的累积梯度上(brown vector)有一个大的跳跃，然后衡量一下梯度做一下修正(red vector)，这种预期的更新可以避免我们走的太快。
NAG 可以使 RNN 在很多任务上有更好的表现。
目前为止，我们可以做到，在更新梯度时顺应 loss function 的梯度来调整速度，并且对 SGD 进行加速。
?
这个算法是对 Adagrad 的改进，和 Adagrad 相比，就是分母的 G 换成了过去的梯度平方的衰减平均值：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
这个分母相当于梯度的均方根 root mean squared (RMS) ，所以可以用 RMS 简写：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
其中 E 的计算公式如下，t 时刻的依赖于前一时刻的平均和当前的梯度：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
梯度更新规则:
此外，还将学习率 η 换成了 RMS[Δθ]，这样的话，我们甚至都不需要提前设定学习率了：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 
超参数设定值:?
γ 一般设定为 0.9。
RMSprop 是 Geoff Hinton 提出的一种自适应学习率方法。
RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的，
梯度更新规则:?
RMSprop 与 Adadelta 的第一种形式相同：
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
超参数设定值:?
Hinton 建议设定 γ 为 0.9, 学习率 η 为 0.001。
? RMSprop借鉴了一些Adagrad的思想，不过这里RMSprop只用到了前t-1次梯度平方的平均值加上当前梯度的
平方的和的开平方作为学习率的分母。这样RMSprop不会出现学习率越来越低的问题，而且也能自己调节学习
率，并且可以有一个比较好的效果。
? ?( SGD不能逃离鞍点问题,速度也比较慢)
我们选优化器的时候可以每一个优化器都试一遍，哪一个优化器最好用就选哪个优化器。也可以看以下参考：
（1）如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。
（2）RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。
（3）Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，
（4）随着梯度变的稀疏，Adam 比 RMSprop 效果会好。
（5）整体来讲，Adam 是最好的选择。
（6）很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点。
如果需要更快的收敛，或者是训练更深更复杂的神经网络，需要用一种自适应的算法
